1. Uitleg in algemene bewoording:
Een gezin heeft gemiddeld 2 kinderen. Dan dan mag je maximaal 12 moeder behandelen om gemiddeld op 24 kinderen uit te komen. En met dit beleid is de kans op meer dan 38 kinderen 1 op een miljoen. Deze zeer kleine kans correspondeert niet met de vele donoren met veel meer dan 25 kinderen. Dit is alleen te verklaren als er beleidsmatig meer dan 12 moeders behandeld zijn. Het excuus dat er gezinnen zijn die toch een tweede kind willen is een argument dat door de statistiek naar het rijk der fabelen wordt verwezen.
2. Wetenschappelijke uitleg:
In de uitleg bij 1 wordt de gezinsgrootte afgerond op 2 kinderen. Volgens het CBS waren er gemiddeld 1,72 kinderen per gezin in 2023. Zie hiervoor de eerste bijlage. Dit geeft een meer precieze berekening zoals onderstaand, maar alle conclusies blijven identiek als bij uitleg 1.
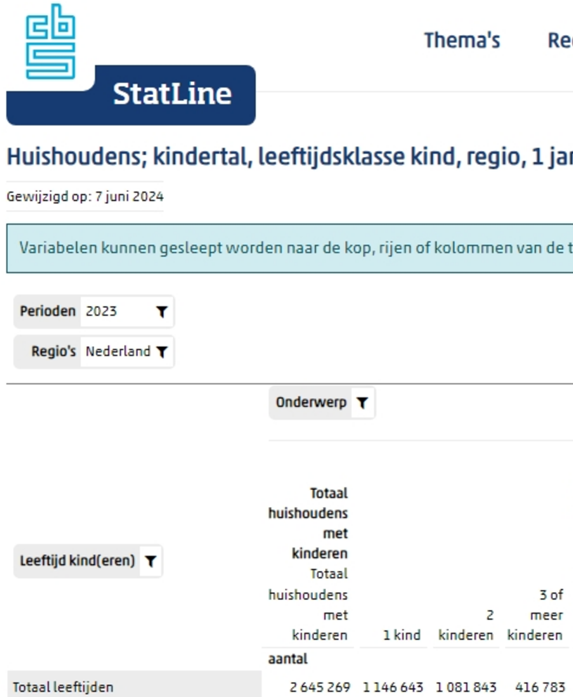
Volgens de CBS-bevolkingsstatistiek waren er in 2023:
2645269 gezinnen met kinderen waarvan:
1146643 gezinnen met 1 kind;
1081843 gezinnen met 2 kinderen;
416783 gezinnen met 3 of meer kinderen. Er wordt met 3 kinderen gerekend!
Dan is de gemiddelde grootte van een gezin met kinderen:
(1146643*1 + 1081843*2 + 416783*3)/2645269 = 1,72 kinderen.
En dan is de standaard deviatie van de gezinsgrootte:
√{ [1146643*(1-1,72)2 + 1081843*(2-1,72)2 + 416783*(3-1,72)2] /2645269} = 0,72.
Voor de nakomelingengroep van een enkele donor geldt dan:
Om op 25 nakomelingen uit te komen mag een fertiliteitscentrum 25/1,72 = 14,5 moeders behandelen. Omdat halve moeders niet bestaan wordt 14,5 afgerond naar 14. Met 14 moeders is het aantal nakomelingen: 14*1,72=24,08 kinderen. Als er 14 moeders behandeld worden met een donor dan is de standaard deviatie van de donor nakomelingen groepsgrootte: 0,72 * √(14) = 2,69.
Hier is de statistische “centrale limietstelling” gebruikt.
En dan nu de klap op de vuurpijl:
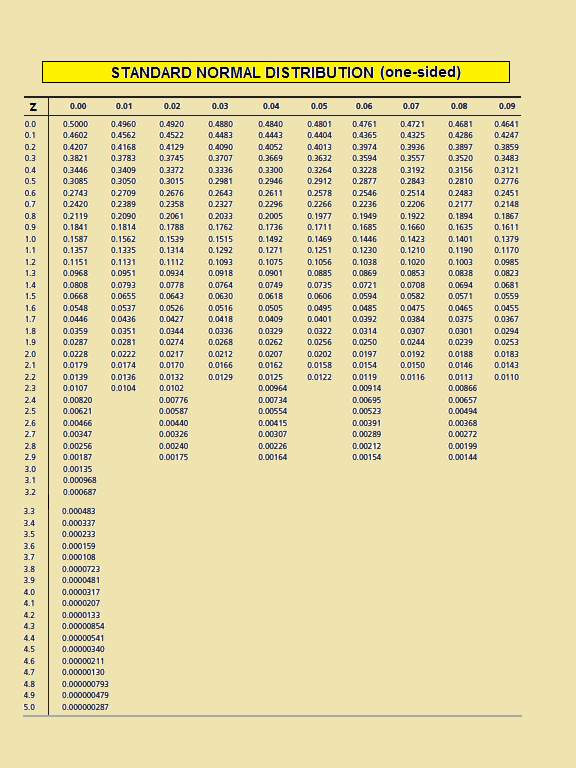
Dan is de kans dat een donor meer dan 38 kinderen krijgt:
Statistiek van de normale verdeling: Z = (38-24,08) / 2,69 = 5,17
Kans: 0,000 000 287.
Zie hiervoor in de tweede bijlage de kansen van de normale verdeling.
Om gevoel te krijgen voor deze kleine kans hieronder wat voorbeelden van kleine kansen
Kans om door de bliksem geraakt te worden: 0,000 005 5.
Kans op een olympische gouden medaille: 0,000 001 5.
*40 Things That Are More Likely to Happen Than Winning the Lottery by Ben Kageyama
Bron (1) – gezinsgrootte volgens het Centraal Bureau van de Statistiek – CBS
Bron (2): De standaard normale verdeling en de kans op een waarneming Z
